QuickSort (qsort) Algorithm
Overview
The quicksort algorithm was discovered by Tony Hoare in 1959.
This algorithm is considered one of the fastest sorting algorithms and shows the best results in most cases.
Here is the algorithm visualization. Below I will describe how it works.
The algorithm works on the “divide and conquer” principle.
Worst case
asymptotic complexity O(n^2)
The answer depends on strategy for choosing pivot. In early versions of Quick Sort where leftmost (or rightmost) element is chosen as pivot, the worst occurs in following cases.
1. Array is already sorted in same order.
2. Array is already sorted in reverse order.
3. All elements are same (special case of case 1 and 2)
It can be fixed by choosing random pivot position
Task
Let’s see how the algorithm works on the example of a simple array of 12 numbers.
[10, 5, 7, 4, 1, 2, 5, 7, 9, 8, 3, 6]
Below I will describe the steps that will show how this algorithm works.
Step 1.
Select “Pivot”. This is the element that will split the array into two parts in the future. On the left side of the pivot, there will be elements that are less than the pivot, and on the right, more or equal. There are many methods for choosing a pivot, and the speed at which the array will be sorted depends on the choice of the pivot. One of the methods for selecting a pivot is to select the last element of the array. Another method is selecting random element, in this case the time complexity always will be O(n log n).
We also need to create a variable “i”, which will point to the first element in the array, which is less than the pivot and at the same time is closest to it. We also need the index of the current element “j”
In our case,
- pivot = 6 (value of the last element in the array),
- i = 0,
- j = 0
Step 2.
Compare the array element with index j with the pivot. 10 > 6. Array elements do not need to be moved.
Change the index “j”.
j = j + 1 = 1
Step 3.
Compare the array element with index j with the pivot. 5 < 6. Swap the elements with indices i and j. Now the array looks like this
[10, 5, 7, 4, 1, 2, 5, 7, 9, 8, 3, 6] –> [5, 10, 7, 4, 1, 2, 5, 7, 9, 8, 3, 6]
Change the indexes
i = i + 1 = 1
j = j + 1 = 2
Step 4.
Compare the array element with index j with the pivot. 7 > 6. Array elements do not need to be moved.
Change the index “j”.
j = j + 1 = 3
Step 5.
Compare the array element with index j with the pivot. 4 < 6. Swap the elements with indices i and j. Now the array looks like this
[5, 10, 7, 4, 1, 2, 5, 7, 9, 8, 3, 6] –> [5, 4, 7, 10, 1, 2, 5, 7, 9, 8, 3, 6]
Change the indexes
i = i + 1 = 2
j = j + 1 = 4
Step 6.
Compare the array element with index j with the pivot. 1 < 6. Swap the elements with indices i and j. Now the array looks like this
[5, 4, 7, 10, 1, 2, 5, 7, 9, 8, 3, 6] –> [5, 4, 1, 10, 7, 2, 5, 7, 9, 8, 3, 6]
Change the indexes
i = i + 1 = 3
j = j + 1 = 5
Step 7.
Compare the array element with index j with the pivot. 2 < 6. Swap the elements with indices i and j. Now the array looks like this
[5, 4, 1, 10, 7, 2, 5, 7, 9, 8, 3, 6] –> [5, 4, 1, 2, 7, 10, 5, 7, 9, 8, 3, 6]
Change the indexes
i = i + 1 = 4
j = j + 1 = 6
Step 8.
Compare the array element with index j with the pivot. 5 < 6. Swap the elements with indices i and j. Now the array looks like this
[5, 4, 1, 2, 7, 10, 5, 7, 9, 8, 3, 6] –> [5, 4, 1, 2, 5, 10, 7, 7, 9, 8, 3, 6]
Change the indexes
i = i + 1 = 5
j = j + 1 = 7
Step 9.
Compare the array element with index j with the pivot. 7 > 6. Array elements do not need to be moved.
Change the index “j”.
j = j + 1 = 8
Step 10.
Compare the array element with index j with the pivot. 9 > 6. Array elements do not need to be moved.
Change the index “j”.
j = j + 1 = 9
Step 11.
Compare the array element with index j with the pivot. 8 > 6. Array elements do not need to be moved.
Change the index “j”.
j = j + 1 = 10
Step 12.
Compare the array element with index j with the pivot. 3 < 6. Swap the elements with indices i and j. Now the array looks like this
[5, 4, 1, 2, 5, 10, 7, 7, 9, 8, 3, 6] –> [5, 4, 1, 2, 5, 3, 7, 7, 9, 8, 10, 6]
Change the indexes
i = i + 1 = 6
j = j + 1 = 11
Step 13.
The “j” index is 11, which is the pivot index. We finish rearranging the elements in this iteration. Now we can split this array into 2 arrays. The left one will contain elements less than the pivot, and the right one is greater than or equal to the pivot. We leave the pivot in the middle between the arrays. It has already taken its place in the sorted array.
The first element of the array in which all elements are greater than or equal to the pivot will be the element with index i. We transfer the pivot in the middle between the arrays.
[5, 4, 1, 2, 5, 3] [6] [7, 7, 9, 8, 10]
Then we sort the resulting 2 subarrays ([5, 4, 1, 2, 5, 3] and [7, 7, 9, 8, 10]) according to the above algorithm. We no longer use pivot “6”. Each subarray will have its own pivot
To make it easier to write, I will describe the steps in the form of a table. You will be able to follow the steps and check the instructions above.
Step 14-19.
Sort the sub-array [5, 4, 1, 2, 5, 3]. pivot = 3; i = 0; j = 0
| Compare | Current array | Procedure | Result array | i | j |
| 5 > 3 | [5, 4, 1, 2, 5, 3] | Do not swap elements. Increment “j” | [5, 4, 1, 2, 5, 3] | 0 | 1 |
| 4 > 3 | [5, 4, 1, 2, 5, 3] | Do not swap elements. Increment “j” | [5, 4, 1, 2, 5, 3] | 0 | 2 |
| 1 < 3 | [5, 4, 1, 2, 5, 3] | Swap elements “i” and “j”. Increment “i” and “j” | [1, 4, 5, 2, 5, 3] | 1 | 3 |
| 2 < 3 | [1, 4, 5, 2, 5, 3] | Swap elements “i” and “j”. Increment “i” and “j” | [1, 2, 5, 4, 5, 3] | 2 | 4 |
| 5 > 3 | [1, 2, 5, 4, 5, 3] | Do not swap elements. Increment “j” | [1, 2, 5, 4, 5, 3] | 2 | 5 |
Step 20-24.
Sort the sub-array [ 7, 7, 9, 8, 10]. pivot = 10; i = 0; j = 0
| Compare | Current array | Procedure | Result array | i | j |
| 7 > 10 | [7, 7, 9, 8, 10] | Do not swap elements. Increment “j” | [7, 7, 9, 8, 10] | 0 | 1 |
| 7 > 10 | [7, 7, 9, 8, 10] | Do not swap elements. Increment “j” | [7, 7, 9, 8, 10] | 0 | 2 |
| 9 > 10 | [7, 7, 9, 8, 10] | Do not swap elements. Increment “j” | [7, 7, 9, 8, 10] | 0 | 3 |
| 8 > 10 | [7, 7, 9, 8, 10] | Do not swap elements. Increment “j” | [7, 7, 9, 8, 10] | 0 | 4 |
We split the array. Now the general array looks like this:
[1, 2] [3] [5, 4, 5] [6] [7, 7, 9, 8] [10]
Then we sort the resulting 3 subarrays according to the above algorithm. It turned out 3 subarrays because in the second subarray ([7, 7, 9, 8, 10]) the pivot was the largest element in the subarray
Step 25.
Sort the sub-array [1, 2]. pivot = 2, i = 0, j = 0,
| Compare | Current array | Procedure | Result array | i | j |
| 1 < 2 | [1, 2] | Swap elements “i” and “j”. Increment “i” and “j” | [1, 2] | 0 | 1 |
We split the array. Now the general array looks like this:
[1] [2] [3] [5, 4, 5] [6] [7, 7, 9, 8] [10]
Step 26-27.
Sort the sub-array [5, 4, 5]. Pivot = 5, i = 0, j = 0,
| Compare | Current array | Procedure | Result array | i | j |
| 5 = 5 | [5, 4, 5] | Do not swap elements. Increment “j” | [5, 4, 5] | 0 | 1 |
| 4 < 5 | [5, 4, 5] | Swap elements “i” and “j”. Increment “i” and “j” | [4, 5, 5] | 1 | 1 |
Step 27-29.
Sort the sub-array [7, 7, 9, 8]. pivot = 8, i = 0, j = 0,
| Compare | Current array | Procedure | Result array | i | j |
| 7 < 8 | [7, 7, 9, 8] | Swap elements “i” and “j”. Increment “i” and “j” | [7, 7, 9, 8] | 1 | 1 |
| 7 < 8 | [7, 7, 9, 8] | Swap elements “i” and “j”. Increment “i” and “j” | [7, 7, 9, 8] | 2 | 2 |
| 9 > 8 | [7, 7, 9, 8] | Do not swap elements. Increment “j” | [7, 7, 9, 8] | 2 | 3 |
We split the array. Now the general array looks like this:
[1] [2] [3] [4, 5] [5] [6] [7, 7] [8] [9] [10]
Step 30.
Sort the sub-array [4, 5]. pivot = 5, i = 0, j = 0,
| Compare | Current array | Procedure | Result array | i | j |
| 4 < 5 | [4, 5] | Swap elements “i” and “j”. Increment “i” and “j” | [4, 5] | 1 | 1 |
We split the subarray. Now the general array looks like this:
[1] [2] [3] [4] [5] [5] [6] [7, 7] [8] [9] [10]
Step 31.
Sort the sub-array [7, 7]. pivot = 7, i = 0, j = 0,
| Compare | Current array | Procedure | Result array | i | j |
| 7 = 7 | [7, 7] | Swap elements “i” and “j”. Increment “i” and “j” | [7, 7] | 1 | 1 |
We split the subarray. Now the general array looks like this:
[1] [2] [3] [4] [5] [5] [6] [7] [7] [8] [9] [10]
The array sorting is finished.
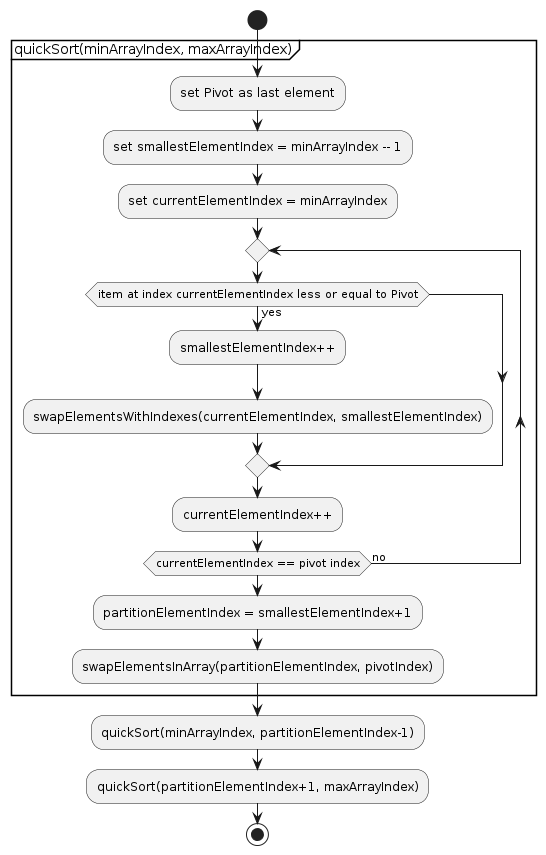
PlantUML diagram of the algorithm
Sample code
Below you will get link to github repo with Kotlin, Java, and Python code


0 Comments