Algorithm for finding the shortest path from one vertex of the graph to all the others.

This algorithm was developed by the Dutch scientist Edsger Wybe Dijkstra in 1959.

The algorithm works only for a directed graph in which the edges have no negative weight and do not have loops. Or is works only with DAG (Directed Acyclic Graph).

Task:

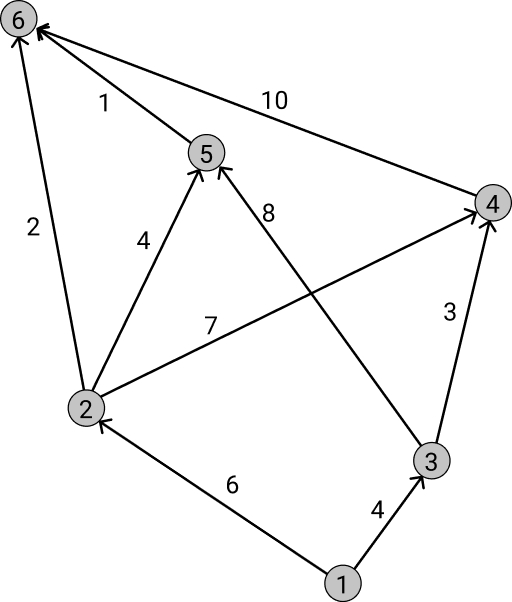
Given a weighted directed graph without negative weight arcs. Find the shortest paths from vertex “1” to all others

Solution

We make a table of distances from the vertex “1” to all the others, including the vertex “1”.

Iteration 0.

Mark vertex 1 as a base vertex. We know that the distance from vertex 1 to vertex 1 is 0. It is less than infinity. We write it down to the table. For the rest of the vertices, for now, write down the distance value equal to infinity. Select the smallest distance value from the first iteration. This is distance 1-1. Vertex 1 is resolved. Moving on to the next iteration

# Iter	Vertex 1 (resolved)	Vertex 2	Vertex 3	Vertex 4	Vertex 5	Vertex 6
0	0	∞	∞	∞	∞	∞

Iteration 1.

From vertex 1 you can go to vertex 2 and 3.
The distance from vertex 1 to vertex 2 will be 0 + 6 = 6 (edge ​​weight 1-2). 6 is less than infinity. We write to the table.
The distance from vertex 1 to vertex 3 will be 0 + 4 = 4 (edge ​​weight 1-3). 4 is less than infinity. We write to the table.
Select the smallest distance value from the first iteration. This distance is from 1-3. Vertex 3 is resolved. It is now basic. Moving on to the next iteration

# Iter	Vertex 1 (resolved)	Vertex 2	Vertex 3 (resolved)	Vertex 4	Vertex 5	Vertex 6
0	0	∞	∞	∞	∞	∞
1		6	4	∞	∞	∞

Iteration 2.

From vertex 3 you can go to vertex 4 and 5.
The distance from vertex 3 to vertex 4 will be 4 + 3 = 7. 7 is less than infinity. We write to the table.
The distance from vertex 3 to vertex 5 will be 4 + 8 = 12. 12 less than infinity. We write to the table.
Transfer the distance value 1-2 to the second iteration without changes.
Select the smallest distance value from the second iteration. This distance is from 1-2. Vertex 2 is resolved. Vertex 2 is now basic. Moving on to the next iteration

# Iter	Vertex 1 (res-d)	Vertex 2 (res-d)	Vertex 3 (res-d)	Vertex 4	Vertex 5	Vertex 6
0	0	∞	∞	∞	∞	∞
1		6	4	∞	∞	∞
2		6		7	12	∞

Iteration 3.

From vertex 2 you can go to vertex 4, 5, and 6.
The distance from vertex 2 to vertex 4 will be 6 + 7 = 13. 13 is greater than 7, which is already in the table. We transfer the value from the previous iteration to the current one.
The distance from vertex 2 to vertex 5 will be 6 + 4 = 10. 10 is less than 12. Write it down in the table.
The distance from vertex 2 to vertex 6 will be 6 + 2 = 8. 8 is less than infinity. We write to the table.
Select the smallest distance value from the third iteration. This distance is from 1-4. Vertex 4 is resolved. Vertex 4 is now basic. Moving on to the next iteration

# Iter	Vertex 1 (res-d)	Vertex 2 (res-d)	Vertex 3 (res-d)	Vertex 4 (res-d)	Vertex 5	Vertex 6
0	0	∞	∞	∞	∞	∞
1		6	4	∞	∞	∞
2		6		7	12	∞
3				7	10	8

Iteration 4.

From vertex 4, you can only get to vertex 6.
The distance from vertex 4 to vertex 6 will be 7 + 10 = 17.17 is greater than 8, which is already in the table. We transfer the value from the previous iteration to the current one.
The distance value 1-5 is transferred to the second iteration without changes.
Choose the smallest distance value from the fourth iteration. This distance is from 1-6. Vertex 6 is resolved. Vertex 6 is now basic. Moving on to the next iteration

# Iter	Vertex 1 (res-d)	Vertex 2 (res-d)	Vertex 3 (res-d)	Vertex 4 (res-d)	Vertex 5	Vertex 6 (res-d)
0	0	∞	∞	∞	∞	∞
1		6	4	∞	∞	∞
2		6		7	12	∞
3				7	10	8
4					10	8

Iteration 5.

From vertex 5, you can only go to vertex 6.
The distance from vertex 5 to vertex 6 will be 10 + 1 = 11. 11 is greater than 8, which is already in the table. We transfer the value from the previous iteration to the current one.
Vertex 5 has been resolved.

All vertices are resolved. The algorithm is complete. The shortest distances from vertex 1 to all other vertices can be seen in the table.

# Iter	Vertex 1	Vertex 2	Vertex 3	Vertex 4	Vertex 5	Vertex 6
0	0	∞	∞	∞	∞	∞
1		6	4	∞	∞	∞
2		6		7	12	∞
3				7	10	8
4					10	8
5						8

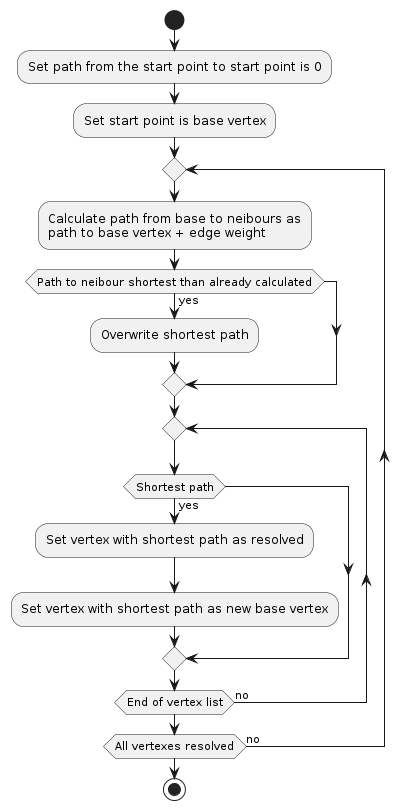
PlantUML diagram of the algorithm

Sample code

Below you will get link to github repo with Kotlin, Java, and Python code